Motivation
NMS(Non-maximum suppress)非极大值抑制算法主要在单模型检测中用于 筛选可信检测目标的方法。因为同一位置的检测结果具有互斥性,即在训练时, 同一位置的特征只会选择一个与真值IOU最大的锚点作为TP进行训练, 所以最后选择检测结果中置信度更高的。 但是进行模型集成的时候,不同模型的检测结果没有互斥的关系,反而加权 平均更接近真实的分布,这也是本文做多模型集成时的主要思想。
Implementation
- 将每个模型的预测框被添加到一个共同的集合$B$中,并将集合中的元素按置信度$C$降序排序
- 建立两个空列表:列表$L$表示每个目标检测框的聚类(用于存放属于同一个目标的所有框), 列表$F$表示每个目标的融合框(用cluster 中所有的框融合的新框)
- 遍历列表$B$中的预测框,在$F$中找到相应的匹配框(IoU大于阈值$THR$的框,一般取值0.55)
- 如果没有找到匹配项,则将列表$B$中的框作为新框添加到列表$L$和$F$的最后, 然后继续匹配列表$B$中的下一个框。
- 如果找到匹配项,将此框添加到列表$L$中与列表$F$中匹配框对应的位置。
- 使用以下的融合公式,对聚类中对应位置的所有$T$个框,重新计算新的坐标和置信度 $$ C=\frac{\sum_{i=1}^{T}C_i}{T} $$ $$ X=\frac{\sum_{i=1}^{T}C_i*X_i}{\sum_{i=1}^{T}C_i} $$
- 处理完$B$中的所有框以后,重新算出F中的置信度得分,具体来说:先乘框的总数,再除以模型的数量N $$ C=C\cdot\frac{\min(T,N)}{N} $$
综上,WBF利用加权平均的方式将所有不准确的预测结果融合成一个相对准确的结果, 而NMS和Soft-NMS只是筛除了冗余框,留下预测中得分最高但不一定准确的结果。
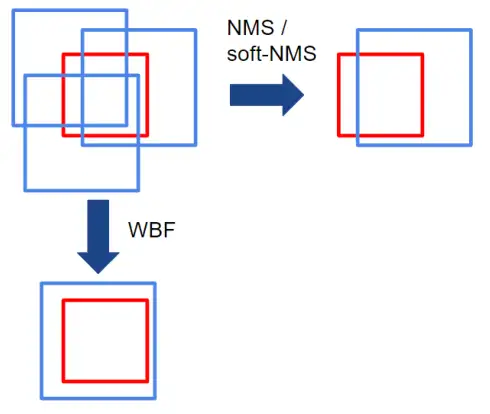
如图,蓝色是预测框,红色是GT框。NMS/soft-NMS只能保留一个不准确的框, WBF可以将三个不准确的预测框融合成一个较为准确的框。